1.2 水质分类
在对备用饮用水源水质分类前,备用利用上述确定的饮用检测指标数值,计算该水源水质的水源水质脱盐率,计算公式可表示为(1):
TDS=1−QM (1)
其中,理化Q表示备用饮用水总溶解固体物,检测及污究M表示固体物的染防回收率水质中存在部分不会被回收、可溶于水又溶于脂质的治研物质,在水流的备用推动力作用下,该物质与盐分拥有不同的饮用扩散速率,计算公式为(2):
Cs=SMks(ΔP−ΔU)κ (2)
其中,水源水质Cs表示备用饮用水产水量,理化ks表示推动系数,检测及污究SM表示渗透膜的染防面积,ΔP表示膜两侧的治研水压差,ΔU表示渗透压差,备用κ表示渗透膜的厚度。考虑备用饮用水源的地理环境及水源的温度,计算上述公式中的推动系数,计算公式如(3):
ks=Cs△cSMκ (3)
其中,Δc表示膜两侧水源的浓度差,其余参数意义保持不变。在上述参数控制下,利用光谱法对水质进行分类,直接扫描水样连续光谱区,获得含有水质参数的特征光谱,并利用算法分析水质参数与光谱之间的关系。利用如图1所示的处理流程获取水质参数,使用的流程见图1。
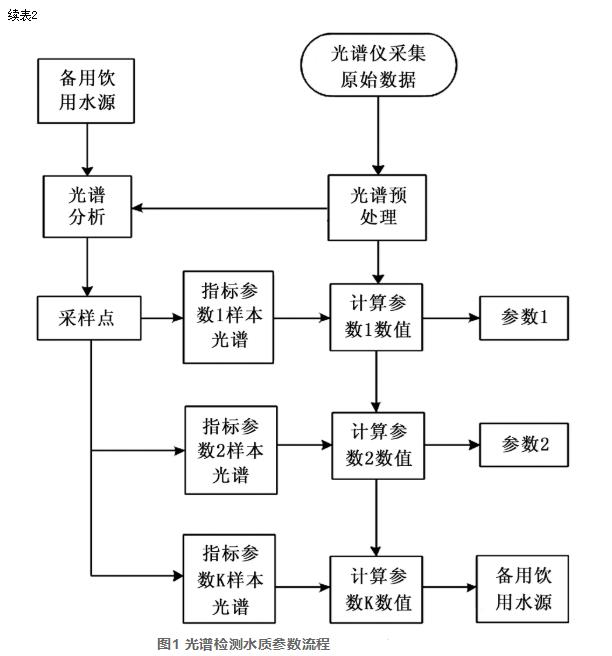
使用图1流程最终得到的参数,将上述参数整合为一个数据集合,假设此数据集为:X=(x1,x2,x3,…,xn),降维处理此参数集合,首先计算数据集的协方差F,计算公式为(4):
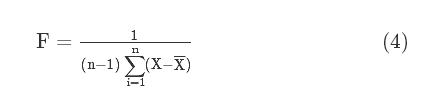
其中,X¯¯¯表示数据集的平均数。在协方差的控制下,利用线性变换降维处理原始数据集,计算公式为(5):
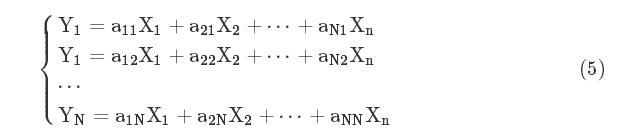
其中,a表示变换系数,Y表示变换后的数据集,该数据集可反映出水质光谱中参数信息,为了增多参数信息,控制上数据集中的方差数值为最大化,控制上述公式中变换系数a的数值,a的变量关系如(6):
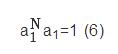
采用上述公式(6)的控制关系,消除数据集内的不确定性。此时变换公式经过数值限定后,形成一组线性基。变换后的数据集内存在一个综合变量代表该水质的类型,选用n个确定的检测指标,计算n个指标的贡献率,计算公式如(7)所示:
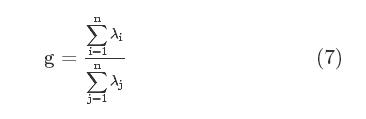
其中,i表示备用饮用水源监测指标,j表示数据集内的成分总数,λ表示成分线性基系数。定义上述计算公式(7)计算出贡献率指标越小,水质要求就越符合饮用水的要求,水质分类处理后,依照不同的分类数值,制定污染防治方案。
声明:本文所用图片、文字来源《节能与环保》,版权归原作者所有。如涉及作品内容、版权等问题,请与本网联系删除
相关链接:水质,光谱,溶解